在这篇论文中，来自国防科技大学和普林斯顿大学的研究者提出了一种面向单张 RGB-D 图像的对称检测网络 SymmetryNet。实验结果表明，该检测网络显著优于其它已有方法，性能达到了 SOTA，尤其是在没有训练过的物体上优势明显。此外，SymmetryNet 能够准确地检测出多种不同物体的对称性，包括被遮挡的物体、包含多个对称面的物体等。

作为大多数物体的基本几何属性，对称性广泛存在于我们的生活中。理解物体的对称性是计算机理解真实世界以及机器人智能交互中的重要问题。因此，对称性检测在图像分割、物体检测以及机械臂抓取等任务中有着广泛的应用前景。

三维物体对称性检测是经典的几何问题，由于对称性具有明确的数学定义（即物体在进行对称变换后具有几何不变性），传统的三维对称检测方法往往首先检测对称对应点（symmetric counterpart），再通过聚类或投****算法得到物体的对称面 / 轴。但是，这类算法的使用范围通常仅限于几何完整的合成三维模型或者高质量的重建三维模型，无法处理物体观测缺失的情况，例如无法通过单张 RGB-D 图像判断物体的对称性。

近日，国防科技大学和普林斯顿大学的研究者提出面向单张 RGB-D 图像的对称检测网络 SymmetryNet，相关论文被 ACM Transactions on Graphics (SIGGRAPH Asia 2020) 收录。

论文链接：https://arxiv.org/abs/2008.00485

数据和代码链接：https://github.com/GodZarathustra/SymmetryNet

方法

不同于从观测数据中检测对称对应点的传统方法，SymmetryNet 从大量数据中学习总结物体对称性出现的规律，进而通过 RGB-D 图像直接预测物体的对称性。

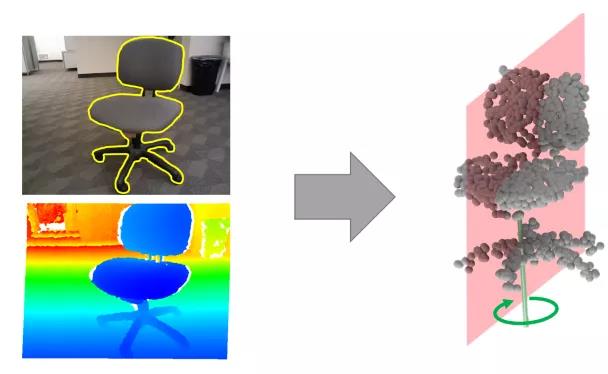
图 1：SymmetryNet：输入 RGB-D 图像，输出物体对称面 / 轴。

其核心思想是在检测物体对称面 / 轴的同时预测输入点云的对称对应点，这样做的好处是能够提高对称检测的精度和泛化能力。SymmetryNet 能够检测物体的反射对称（reflectional symmetry）和旋转对称（rotational symmetry），并且能够自动判断物体对称面 / 轴的数量，实现动态多输出。

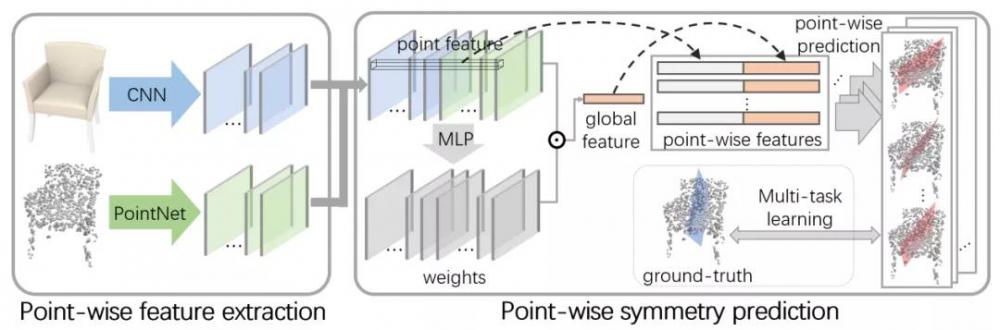
图 2：SymmetryNet 网络结构。

SymmetryNet 包括特征提取和对称性预测两个模块。RGB 图和点云首先分别经过一个卷积神经网络和点云处理网络，得到逐点特征，逐点特征随后通过 weighted average pooling 层计算得到全局特征。逐点特征和全局特征拼接之后被用来预测物体对称面 / 轴。

SymmetryNet 的创新点之一是将物体对称面 / 轴的预测和对称对应点预测结合起来，对这两个相互关联的任务同时训练，从而提升对称检测的精度和泛化能力。如下图 3 所示，对于当前点 P_i，网络不仅预测物体的对称面 / 轴参数 O_i 和 n_i，同时还预测点 P_i 的对称对应点。其中，反射对称物体的对称对应点为 Q_i，旋转对称物体的对称对应点则为一个围绕对称轴的圆环。

此外，为了处理具有多个对称面 / 轴的物体，SymmetryNet 每次输出多个对称面 / 轴，再利用分类器判断输出每一个输出的有效性。对于含有多个对称面 / 轴的物体，SymmetryNet 通过求解 optimal assignment 优化方程计算预测对称面 / 轴与真值的匹配关系，进而计算 loss 并进行回传。

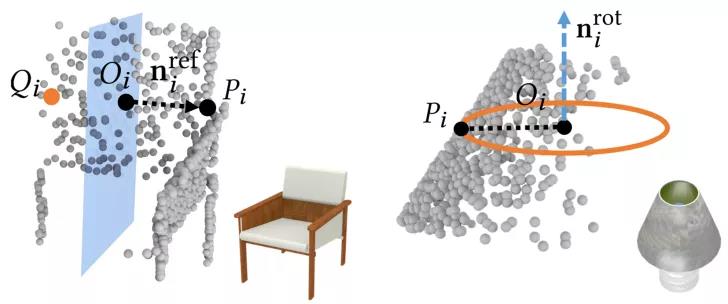
图 3：SymmetryNet 同时预测对称面 / 轴（蓝色部分）以及对称对应点（橙色部分）。

实验

为了验证算法有效性，SymmetryNet 在多个数据集上进行了实验测试，实验选用 PR 曲线作为评价标准。其中，ShapeNet 数据集上的定量实验结果如下图 4 所示。从图中可以看出，SymmetryNet 显著优于其它已有方法，性能达到了 state-of-the-art，尤其是在没有训练过的物体（Holdout category）上优势明显。

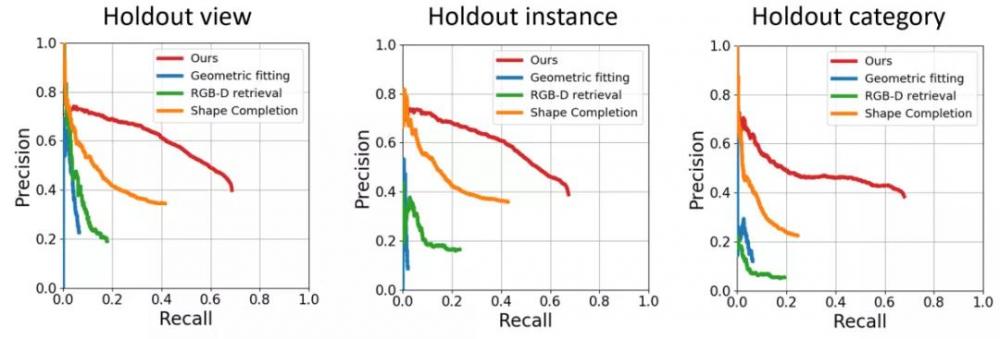
图 4：SymmetryNet 在 ShapeNet 数据集上的测试结果。

下图 5 展示了若干个对称性检测结果，可以看出 SymmetryNet 能够准确地检测出多种不同物体的对称性，包括被遮挡的物体、包含多个对称面的物体等。

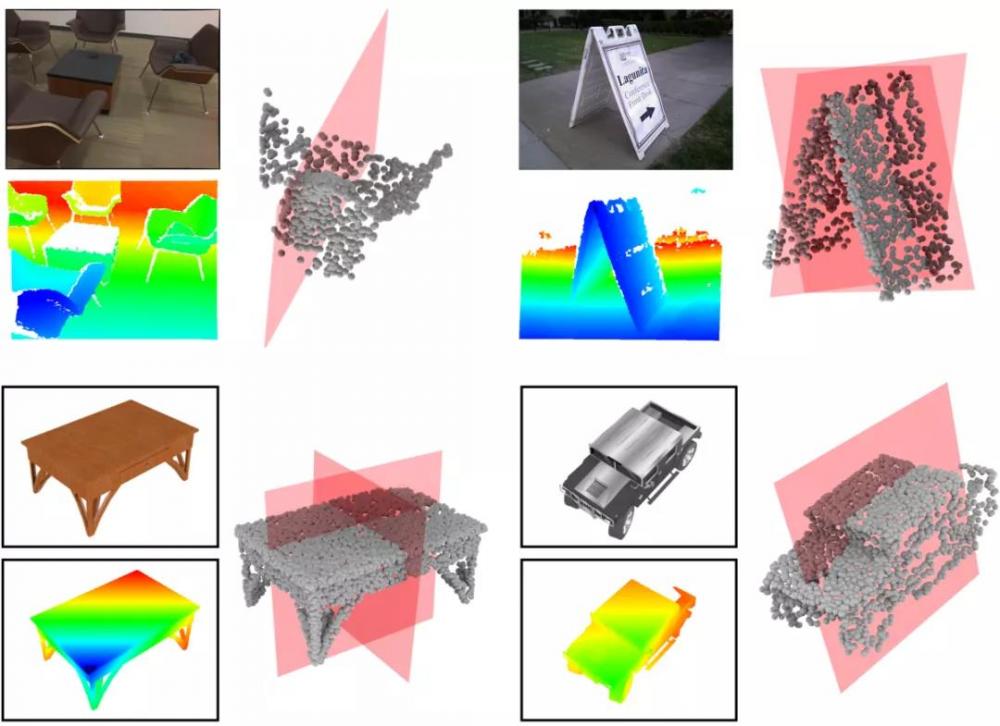
图 5：SymmetryNet 对称性检测结果。

对称性是连接几何和语义的桥廊，理解分析物体对称性是计算机感知真实世界的重要方式。因此，对称检测可以为计算机视觉、机器人学中的多种任务提供理论和信息支持，具有十分广阔的应用前景。将图像分割、形状补全、位姿估计、机器人抓取等任务与对称检测结合，有望实现精度更高并且更加鲁棒的算法。

此外，研究实现高效的对称数据标注方法，或者实现对称检测网络的自监督训练，对于该研究方向同样具有重要意义。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。